Q 7-16:数学学習の特色をお聞かせください。
学校からの回答
中2ではチームティーチング、中3では習熟度別授業を行っています。
少人数クラスで行います。
テキストは「体系数学」を使用し、高校受験がない分の時間などにより、高校の分野も少し学習します。
中学では,豊富な授業時間(中1は週5回,中2・3は週6回)をもとに,こまめに学習状況をチェックしながら基礎学力をつけていきます。「体系数学」を用いることで,指導要領では学年をまたいだ内容も一気に扱うなど,効率的で効果的に学習を進めることができるため,中3の1学期には高校の内容に入る「ゆとりある先取り教育」を実施することができます。高校では高1での習熟度別授業,高2からの文理コース選択によって,生徒それぞれの学力に応じた指導を行っています。理系は高3の1学期に教科書の内容を終え,大学受験のための問題演習に十分な時間をとることができるようになっています。
また,本校数学教育のもう一つの特徴は,「数学が世の中にどう役立っているか」を折に触れて伝えていることです。特に中3では週1回「数学総合」という授業にて,校舎の高さの測量や作図による震源地の特定など,実社会における数学の適用例を多く採り上げ,生徒自身で手を動かし,考えることで,数学の有用性が体感できるようにしています。
数学はスタディサプリを活用した反転学習を行っています。
学校では演習を中心とした指導を行っています。
基本を大切に授業を進めています。進度を速める授業ではなく、深度を深める授業を心がけています。
独自プリントを使用しての協働学習
先取り、丁寧な指導、グループワークと個人ワークのバランス
中高6年すべての数学の授業がハーフクラス
週に1日「数学デー」を設けて、放課後に質問対応や課題未了の生徒をサポート
習熟度別クラス編成。数検取得に向けた対策講座。検定外教科書の使用。
中学校では、計算トレーニングなどの基礎を重視します。
中学の全学年で数学科が他教科とコラボして探求授業「MathQuest」を展開しています。
中学3年から習熟度別に授業を行います。
夏期特別学習・冬期特別学習や放課後等の講習で大学受験問題に取り組んでいます。
中学生は中学1年生より少人数・習熟度別に分かれて授業をおこなっています。
高校ではコースごとに細かく授業が分かれることもあり、少人数で授業がおこなわれることがあります。
また、数検(実用数学技能検定)を、校内で年度に3回受験することができます。
単純な解法指導や公式の暗記ではなく、本質を見極めて理論的に解にたどりつけるよう工夫しています。
iPadを活用し、インタラクティブな学習形態を取り入れています。
代数と幾何に分けて授業が行われ、朝の学習時間等を利用して小テストも定期的に行われています。また、グループ学習やタブレットPCを用いてグラフや図形を描く授業も行われています。
基礎から丁寧に学力を積み上げていきます。6年間、連続して学習できるというメリットを存分にいかします。
生徒の発案・思考を重視し、実践するためにICTを活用し、コミュニケーションを重視した学習を実施しています。
中学はいずれの学年も1組2組ともに同じ曜日の同じ時間に授業があるように時間割を組んでいるため、適宜合同授業が可能であり、実験や発表形式もしやすくなっています。
また、大学受験指導においてはより少人数の授業になるため、その生徒の志望校に応じた授業を組み立てることが可能です。
体系数学を使っていますので、無駄なく進めることが出来ています。
また、1年次から代数分野と幾何分野に分け、並行して進めています。
アクティブラーニング型の授業も行っています。
授業内テストを多く行い、合格点に達するまで何度も再テストを繰り返します。これを何度も繰り返すことで、できなかったことをできるようにしていきます。
高校では数学的思考を楽しむような数学ゼミも開講しており、数学が好きな生徒は積極的に参加しています。


全員が中学範囲をすべて使いこなせるよう過度な先取りはせずに進行し、単元ごとに教えあいの時間を設けて全員が理解できていることを確認していきます。
能力が高い生徒は放課後にハイレベルな内容を含む補習に参加できます。
高1段階の数学は習熟度別に授業を実施します。
中学は代数と幾何に分かれて授業
代数は、積み上げ型の分野であるため、「理解~練習~小テスト~振り返り」の繰り返しを徹底する
特に男子はスピードやペースが個々人で大きく異なるため、自分のペースで進めるように比較的遅めに進める。その分、はやい子達には発展問題プリント(高校入試レベル)を解けたら次、解けたら次、と先に進める仕組みをとっている(中1・中2)
幾何は、STEAMの基礎として、デザイン・統計・論理を学ぶことを意図とした授業となっている。平面図形では好きな図形を作図したり、空間図形ではポリドロンをつかった図形デザインを行う。統計では自分でデータを取得し、その分析レポートを提出する「統計グラフコンクール」を行う。図形の証明では、論理的思考力を高めるために、独自のプリント・メソッドをもとに論証のための根拠を組み立てる練習を行う

問題解決型授業を取り入れ、論理的思考力を育みます。
中学校になると算数が数学になります。
算数と数学の最も大きな違いは、数学では文字式を扱うことです。
つるかめ算は連立方程式に変わります。
具体的な数から抽象的な数へ、有限から無限へ数の世界が広がることが、算数から数学への変化だと言えるでしょう。
無限という新たな考えを受け入れ、想像を働かせることができるようになれば、世の中のどんなことも恐れずに対応できるようになるはずです。
中学校
アース・プロジェクトや行事など、学校生活で感じた疑問をiPadを使って集めています。こうした疑問を疑問のままで終わらせるのではなく、数学的な問題に置き換え、日頃の疑問を自らの力を使って数学的に解決するための授業を行っています。もちろん、数学を用いた解決だけでは難しい問題も多数出てきますが、そのときは、数学のみにとらわれず、すべての教科と連携をとり、解決に向けた指導をしています。そして、新たな取り組みとして問題解決のプロセスを自由研究のコンクールに出品し、生徒の表現力を高めていきます。
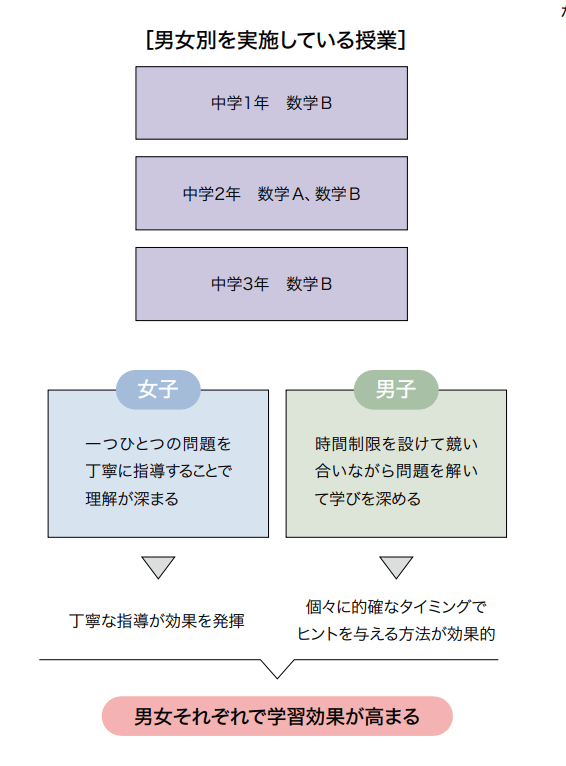
なお、中学の数学の授業に関しては、男子と女子では空間把握能力や計算的思考力の特性や、自信をつける上で効果的なアプローチ(例:男子は問題演習中心にするほうが自信がつくが、女子は少し時間をかけて理詰めで説明していったほうが自信がつくなど)に違いがありますので、一部を男女別に実施しております。
高等学校
数学はわかると楽しい、解けると楽しい、できるようになると楽しい科目です。本校では、「数学を数楽に」をテーマとして掲げ、生徒が自分自身で問題解決できる力を養うための授業を展開しています。そのためには、予習として教科書やスタディサプリを使って生徒自身に理解してきてもらい、その理解が正しいかどうか、定着しているかどうかをiPadを使って生徒と教員がやり取りしながら確認することもしています。大学入試改革の中で、数学では「日常生活や社会現象の問題を数学的に表現し、解決する」という力が求められるようになります。本校では、学習進度を早めることによって問題演習の時間を多く取り入れ、数学の問題を自分の言葉で表現し、解決する力を育みます。
低学年は宿題や小テストを活用して学習習慣を身につけます。中3・高1では習熟度別授業を通して自分の特性や進路を考える時としています。高2・高3の選択科目では大学受験に向けて集中した勉強をします。どの学年もテストの振り返りや再試などきめ細かく指導。長期休みにはハイレベル講習を実施しています。
2クラスまたは3クラスを3~4コースに分けて習熟度別で授業を行っています。数学は理解の差が明確に出るので、少人数で指導することにより生徒の理解が深められるように授業を行っています。
学習の特徴として統計分野にも力を入れています。データからどのような結果が得られるのか表にまとめたり、発表したりする機会を設けています。それは自由研究や国語のディベートにも活かされています。コース分けは定期考査後、日常学習点とテスト点の総合で行います。
数学学習の特徴は2点あります。
1点目は先取り学習の実施です。
中学3年次に高校数学の先取り学習を行っています。これにより、高校3年次に演習時間を多く確保することが可能です。特に文系生徒は高2の間に教科書の内容を修了します。また、理系特進クラスは高3の1学期に教科書を終えます。
2点目は数学演習という科目です。
この科目は数学の授業の復習や発展的な内容を学習していく授業です。基礎基本の定着を行い、更に思考力や応用力を鍛えていく授業になります。
数学のおもしろさが伝わるように、ていねいな授業を展開しています。
苦手意識を払拭させるために、生徒同士の教え合いの時間を取り入れています。先に理解した生徒が教えることで苦手な生徒にも分かり易く、また教える生徒の理解がより深くなる効果があります。
朝学習の実施や、各学年で週5時間の授業を充て、基礎学力定着のための時間を確保しています。また、実験を行うなどして数学への興味を持てる授業を展開しつつ、中高6年間の数学の土台となる基礎計算の定着を重視しています。
中2から高1までは習熟度別に授業を行い、特に中学では少人数できめ細やかな指導を行います。
苦手意識を払しょくするため、パズルやグラフ描写ソフトを用いるなど抽象的なものを具体的に表現することをこころがけています。また、興味関心を伸ばすため、理科や芸術科と教科横断型授業も実施しています。
数学の授業では、アクティブラーニング型授業を展開し、次の「6つの力」を学年・単元に合わせて徐々に深化させていきます。
①情報を正確に理解する「読解力」
②知識を活用する「思考力」
③感覚的に推測できる「直観力」
④正確に処理する「計算力」
⑤考えを筋道立てて伝える「表現力」
⑥問題を作成できる「作問力」
これらの力を育成する活動を通して、将来待ち受けるさまざまな課題に対して、現象を数理的にとらえ、論理的な思考を駆使し、課題の解決に貢献できる人材を育てていきます。 また、18年間続く伝統の「桐蔭数学学力試験(通称:トーマスオリンピック)」では、年2回、教員オリジナル問題に3時間かけて挑戦します。1年から6年までの生徒が同じ問題に取り組むことで、学年や分野に関係なく「自由な発想で解く」ことを主眼に置いて実施しています。
「探究(未来への扉)」という授業です。
1年次から5年次に週に1回「未来への扉」という科目名の探究の授業があります。この授業では、情報の集め方、情報の整理の仕方、プレゼンテーション資料の作り方といった基礎的なスキルから、さまざまな角度からの分析の仕方、問題解決の方法など一生涯使える力を身につけます。
習熟度で分けて細やかな指導を行います。
数学は、今年度から検定教科書を使用しますが、長い間「マイスター」という教科書を使っていました。検定教科書にない内容や発展させるべき点については、長年の蓄積がありますので、随時補填していくという指導に変えます。当然、今までと同様、高校内容も入ってきます。
補習が多いです。
解法を身につけること以上に、問題の本質を理解することを重視しています。また、Libryという学習支援アプリを活用しています。問題演習の正答率や間違い方をもとに、自分に適した問題をAI(人工知能)が選択し、解き方のヒントを提供するものです。これにより、同じ授業の中で数学が得意な生徒は発展問題に取り組み、苦手な生徒は前に戻って学習する、ということを可能にしています。
基礎能力はアプリを使って個別最適化。授業ではクリエーションを取り入れ、他分野への広がりを重視しています。
生徒自らが考え、答えを導き出す過程を大切にしています。授業の中で、皆で考え、疑問を解決、納得して理解を深めます。丁寧に反復練習を重ね、着実に基礎力を固めています。毎授業ごとに提出するプリントやワークを通して一人一人きめ細かく指導し、定着をはかります。教員は、提出物のチェックを細かく行い、生徒と何度もやりとりをします。休み時間には、自ら質問に生徒で研究室は溢れています。
重要項目を繰り返し学習する重層的な学びが特色です。可能な限り先取り学習も展開しています。
日出学園の中で最も先取りを行っている教科です。
数学が好きな生徒にとっては楽しいです。
数学な苦手な生徒は習熟度別になってから個別で丁寧に教わります。
中2までは数学の基本的な考え方と計算力を丁寧に指導する中、家庭学習のための学習方法の習得にも力を入れています。その後、中3からは少人数授業により、高校数学の基礎を作る細やかな授業を展開しています。
中学では体系数学を用いて中3次には高校の内容まで履修します。
高校特進コースでは理数クラスを設定し高校数学の範囲を早い段階で履修を終えます。
電子黒板などを使用したり、iPadで進めたりしています。
本郷数学基礎学力検定試験というものがあります。長期休暇明けに行うテストで、得点によって級や段が認定されます。成績上位者は校長から表彰があります。(写真は本数検表彰)

中学では代数分野と幾何分野に授業を分けて、基礎学力の定着に力を注ぎます。高校では必修として高校2年生(数Ⅱ)まで学び、進路選択の幅を広げます。
中学3年間で論理的な思考力を確実に習得することに重点を置き、各単元ごとに確認テストを実施。
少人数で構成する習熟度別授業で、手厚い指導をおこなう。
中学2年間で3年間の内容を習得します。それには生徒の予習・復習の他に、チャックテストを行い、完全習得を目指しております。習得ができていなければ補習を行いわかるまで教えていきます。
希望者は朝学習を行うことがあります。中1と中3は週1回習熟度別授業を実施しています。
教科ポリシーに基づいた学びを展開しています。
■教科ポリシー
様々な未知の問題に対して、自分の思考力・判断力で解決に向かっていける力の育成を目指しています。
そのために、基盤となる基本的学力・知識の定着と、それらをもとに学びを深める活動を実践しています。
■授業展開
・ 学力や知識を習得すべく積極的に学習に取り組み、また得られた知識をもとに、新たな問題を適切に理解する読解力、解決に至るまでの思考力を育てる
・ 自分自身の活動を振り返りながら独力で答えを導く力を育み、また協働活動によるコミュニケーションを通して、自分の考えを論理立てて伝える表現力と、また他者の考えを受け入れる協調性を育てながら、より深い学びを実現する